von Kurt Mahr

Der Autor utopischer Romane sieht sich oft vor das Problem gestellt, die Verhältnisse in der Umgebung ferner, unbekannter Sonnen (Fixsterne) zu schildern. Dabei wird manchmal übersehen, daß zwischen der Farbe eines Sternes und seiner Oberflächentemperatur ein wohlbekannter Zusammenhang besteht. Sterne strahlen nämlich als "schwarze Körper" im Sinne der Physik und das Spektrum der "schwarzen Strahlung" hat eine charakteristische Form (siehe Abbildung), die allein von der Oberflächentemperatur des Strahlers bestimmt wird.

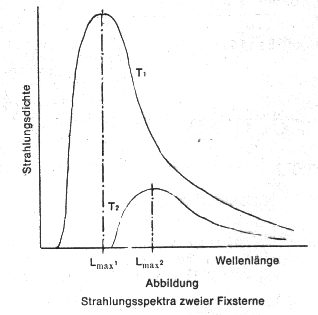
Die Abbildung zeigt schematisch die Spektra zweier Sterne, deren Oberflächentemperatur T1 und T2 betragen, wobei T1 größer ist als T2. Die beiden Kurven zeichnen die Dichte der bei der jeweiligen Wellenlänge abgegebenen Strahlung als Funktion der Wellenlänge. Es ist zu beobachten, daß der Punkt höchster Strahlungsdichte, Lmax1, für den heißeren, der beiden Sterne bei einer geringeren Wellenlänge auftritt als der entsprechende Punkt Lmax2, des kühleren Sterns. Diese Gesetzmäßigkeit faßt das Wien'sche Verschiebungsgesetz wie folgt zusammen:

          Lmax * T = 28.800.000

Dabei ist Lmax wiederum die Wellenlänge, bei der die Strahlungsdichte ihren höchsten Wert erreicht, und wird üblicherwiese in Angström-Einheiten (A) angegeben. Ein Angström ist der zehnmillionste Teil eines Millimeters. T, und zwar in Grad absolut oder Grad Kelvin, ist die Oberflächentemperatur des Sternes. Für unsere Zwecke ist eine abgewandelte Form der Gleichung günstiger, da sie die gwünschte Temperatur unmittelbar als Ergebnis auswirft.
Sie lautet:

          T = 28.000.000 / Lmax

Darauf ein Beispiel: Das Strahlungsmaximum unserer Sonne liegt bei Lmax = 4.800 Angström. Setzen wird diesen Wert in die zweite Gleichung ein, so erhalten wir für die Temperatur an der Sonnenoberfläche den Wert T = 6000° absolut. Diesen Wert kennen wir aber alle schon aus der Schulzeit.

Zur Anwendung der Gleichung seien im folgenden noch einige zusätzliche Erläuterungen gegeben. Das sichtbare elektromagnetische Spektrum, allgemein "Licht" genannt, nimmt den Wellenlängenbereich von 4000 bis 7200 Angström ein. Die Farben sind etwa wie folgt verteilt:

	FARBE	Wellenlängenbereich
	Violett, Blau	4000 - 4800 Angström
	Grün	4800 - 5600 Angström
	Gelb, Orange	5600 - 6000 Angström
	Rot	6000 - 7200 Angström

Nach kürzeren Wellenlängen hin schließt sich der Spektralbereich des Ultravioletten an, nach höheren Wellenlängen hin folgen die Bereiche des Infrarot und der Wärmestrahlung.

Bei der Bestimmung der Farbe eines Fixsterns ist offensichtlich Vorsicht geboten. Nach dem oben Gesagten liegt das Strahlungsmaximum unserer Sonne bei 4800 Angström, also an der Grenze zwischen Grün und Blau. Trotzdem erscheint uns die Sonne gelblich-weiß. Es ist also nicht so, daß die Lage des Strahlungsmaximums allein die Farbe des Sterns verrät. Dem Verlauf der Kurven in der Abbildung ist zu entnehmen, daß die Gesamtstrahlung eines Sternes in weitaus höherem Maße aus Wellenlängen zusammengesetzt ist, die größer sind als Lmax, denn aus solchen, die kleiner sind. Obwohl die Strahlungsspitze unserer Sonne an der Grün-Blau-Grenze liegt, überwiegen in der Gesamtstrahlung schließlich doch die gelb-bis-roten Töne, und in der Mischung entsteht das bekannte Gelb-Weiß.

Sterne, deren Strahlungsmaximum gegenüber dem der Sonne nach kürzeren Wellenlängen hin verschoben sind, werden bei kleineren Unterschieden rein weiß, bei größeren dagegen immer mehr bläulich erscheinen. Die Oberflächentemperatur nimmt dabei nach der Gleichung ständig zu. So zum Beispiel hat der bläuliche Sirius eine Oberflächentemperatur von 11.200° absolut, was einem Wert Lmax = 2500 Angström entspricht, und die noch bläulichere Beta-Centauri mißt an ihrer Oberfläche 21.000° absolut mit einem entsprechenden Lmax von 1333 Angström. Bei beiden Sternen liegt also das Strahlungsmaximum bereits außerhalb des sichtbaren Bereichs im Ultravioletten. Auf der anderen Seite erscheinen Sterne, deren Strahlungsmaximum gegenüber dem der Sonne nach größeren hin verschoben ist, immer gelblicher, dann gelblich-röter und schließlich rot. Beteigeuze zum Beispiel, ein M2-Stern, ist von rötlicher Farbe. Ihr Strahlungsmaximum liegt bei rund 10.000 Angström, also bereits im Infraroten, und ihre Oberflächentemperatur beträgt kanpp unter 3000° absolut.

Zum Abschluß noch eine Bemerkung, die manchem von uns nützlich erscheinen mag: Aus der gesamten Strahlungsleistung eines Fixsterns lassen sich Schlüsse ziehen auf die Licht- und Temperaturverhältnisse an der Oberfläche von Planeten, die diesem Fixstern umkreisen. Gewöhnlich bedient man sich dabei nicht absoluter Werte, sondern man sagt: Dieser Stern strahlt viermal soviel Energie ab, wie die irdische Sonne, die Strahlung liegt annähernd im selben Spektralbereich - wieviel Energie erhält also ein Planet, der von diesem Stern zweimal soweit entfernt ist wie die Erde? Antwort: Ebensoviel. Denn die aufgefangene Strahlungsleistung nimmt mit dem Quadrat der Entfernung ab, so daß folgende Beziehung besteht:

          Wx / We = (re² / rx²) * (Sx / Sa)

Dabei sind:

	Wx	Strahlungsleistung, die ein hypothetischer Planet im Abstand rx von einem Fixstern mit der Strahlungsleistung Sx empfängt.
	We	Die auf der Erde von der Sonne (Abstand re) empfangene Strahlungsleistung.
	Sa	Die Strahlungsleistung der Sonne